Think Multiplication: A Smarter Way to Learn Division
TL;DR: Division facts can be tricky for many kids, but there's a simple trick: teach them to “think multiplication.” By leveraging the close relationship between multiplication and division, children learn to find the answer to a division problem by recalling a multiplication fact they already know. This strategy builds on what they’ve mastered (multiplication) to make new learning (division) much easier, boosting confidence and understanding.
Why Division Facts Feel So Hard
Once addition and subtraction are in the rearview mirror, multiplication and especially division often become a new hurdle. Division facts (like 36 ÷ 6 or 49 ÷ 7) can be intimidating because they are typically presented as separate “tables” to memorize. In truth, division is inherently connected to multiplication – it’s the inverse operation. Yet many children initially approach division as a totally new, unfamiliar task. This can make division facts feel harder to learn than multiplication facts.
Memorizing dozens of division facts in isolation can overwhelm many kids, especially those who thrive on understanding rather than brute-force memory. The good news is that there’s a more intuitive way to master these facts – one that taps into knowledge your child already has. Studies have found that children can perform basic division-like reasoning (such as fair sharing of objects) even before they learn formal division in school, suggesting an intuitive grasp of the concept that we can build on (Szkudlarek et al., 2022).
What Does “Think Multiplication” Mean?
“Think multiplication” is a simple but powerful strategy: when faced with a division problem, the child reframes it as a multiplication question. Essentially, instead of directly asking “What is 20 ÷ 4?”, we encourage them to think “4 times what number equals 20?” By doing this, a division problem is transformed into a familiar multiplication fact-finding exercise. For example:
- Instead of trying to recall 20 ÷ 4 outright, the child asks: “What × 4 = 20?” Since they know 4 × 5 = 20, they can conclude that 20 ÷ 4 = 5.
- If they see 56 ÷ 8 and aren’t sure, they flip it around: “8 times what makes 56?” Realizing 8 × 7 = 56 gives the answer 56 ÷ 8 = 7.
In essence, every basic division fact has a twin multiplication fact. Children often find it easier to remember or derive the multiplication, and once they have that, the division answer comes naturally. This strategy works because most kids find it more straightforward to build up (multiply) than to break apart (divide) – a phenomenon noted even in cognitive research with adults. In one study, adults solving division problems often recast them as multiplication problems (LeFevre & Morris, 1999), essentially thinking of 56 ÷ 8 as “8 × 7 = 56” to get the answer. So when we teach children to do the same, we’re actually aligning with how the brain naturally prefers to work!
Why “Think Multiplication” Works So Well
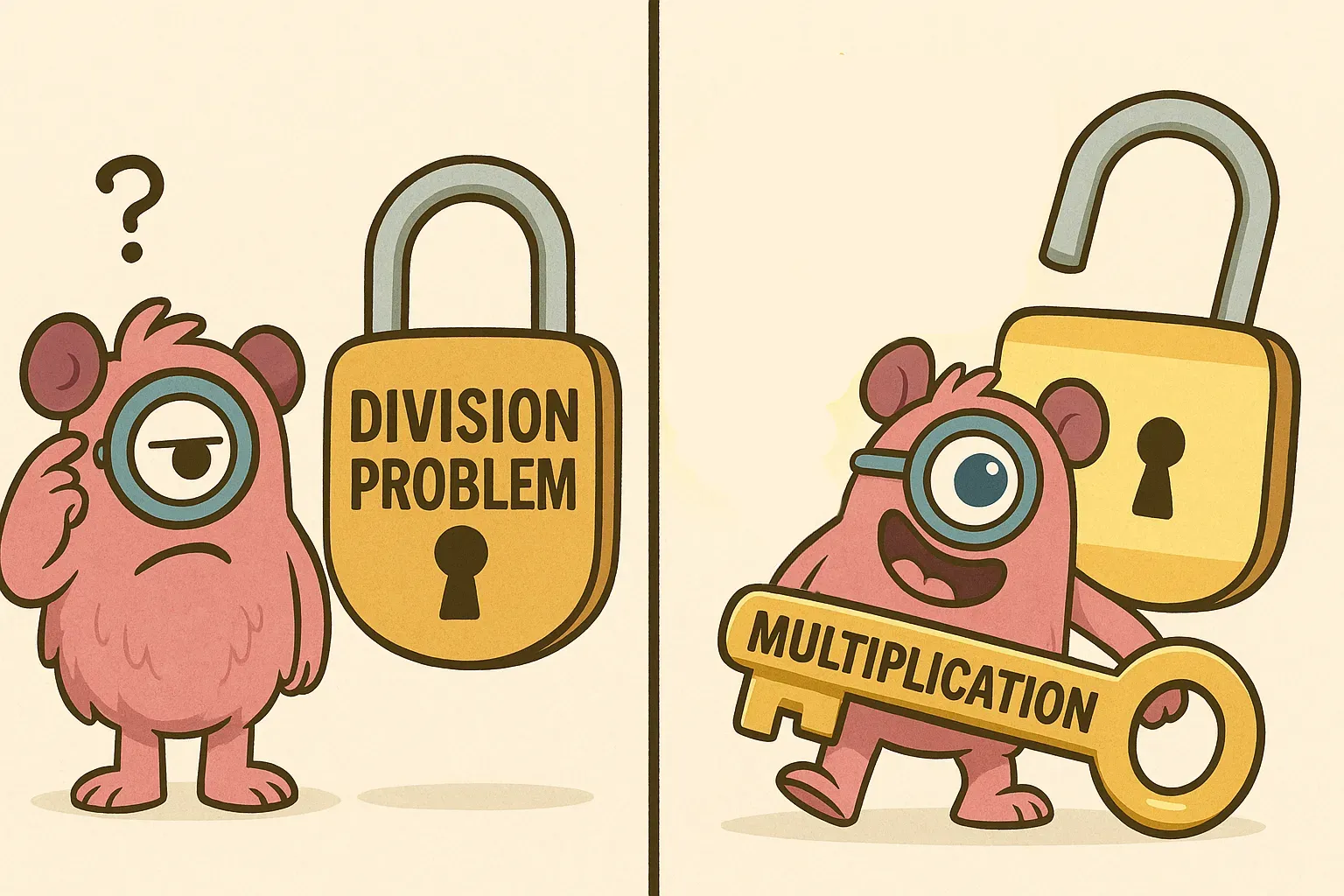
The magic of this approach lies in the inverse relationship between multiplication and division. Math educators emphasize that because multiplication and division are inverses, using multiplication facts is one of the most effective ways to master the division facts. In other words, if your child knows their multiplication facts, they already have a built-in “cheat sheet” for division.
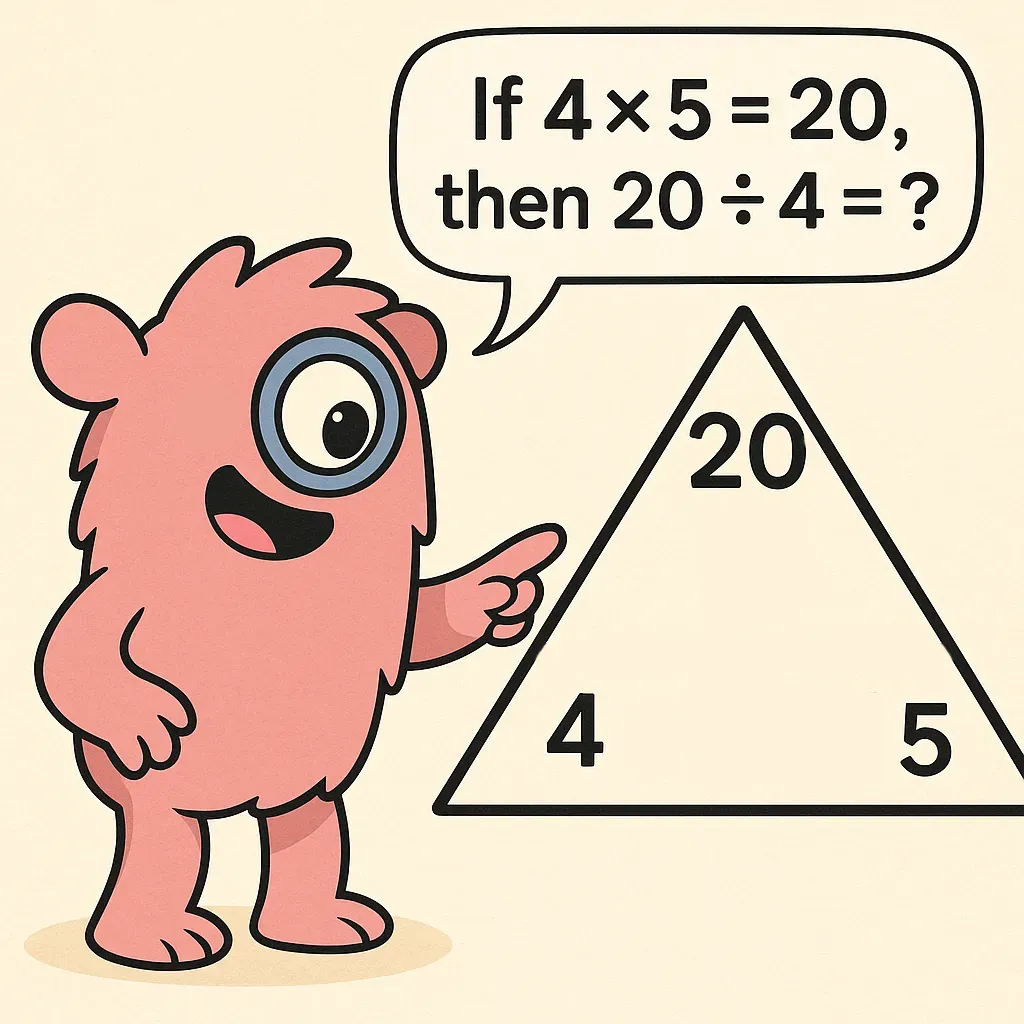
This strategy drastically cuts down the amount of brute memorization needed. Without it, a student might try to memorize that 5 × 4 = 20, 4 × 5 = 20, 20 ÷ 5 = 4, and 20 ÷ 4 = 5 as four separate facts. In reality, these are all part of one fact family. A fact family is a set of related multiplication and division equations using the same numbers. For instance, 4, 5, and 20 form a family: knowing one fact in the family unlocks the others. By thinking multiplication, we reinforce this connection and lighten the cognitive load on kids.
Furthermore, “think multiplication” emphasizes understanding over memorization. It helps children see multiplication and division as two sides of the same coin, rather than unrelated operations. When children understand the connection (for example, that division “undoes” multiplication), they gain a stronger number sense and are less likely to forget their facts. This approach is widely recommended by math education experts and supported by research – even official curriculum guidelines encourage using multiplication knowledge to teach division. In short, “think multiplication” builds a conceptual bridge that makes learning division facts faster, easier, and more meaningful.
How to Teach Your Child to “Think Multiplication”
Here are some practical steps and tips for caregivers and educators to implement this strategy:
- Ensure a solid grasp of multiplication basics: It sounds obvious, but the first step is making sure your child is comfortable with the multiplication facts for their grade level. They don’t need every fact memorized perfectly, but they should understand multiplication as repeated addition or grouping and know at least some key facts (like the 2s, 5s, 10s, etc.). The more multiplication facts they have at their fingertips, the easier division will become.
- Practice the “flip it” approach: Whenever a division fact comes up in homework or daily life, guide your child to flip it into a multiplication question. You can model this by thinking aloud. For example: “Hmm, 36 ÷ 6... let’s flip that around. 6 times what equals 36? Oh, 6 × 6 = 36, so the answer is 6.” Encourage them to always ask themselves that internal question: “___ times what = (the big number)?” This habit takes a little time to form, but soon they'll start doing it automatically.
- Use visual aids and grouping objects: Especially for younger learners, concrete objects can reinforce the concept. You might say: “Let’s show 20 ÷ 4 with pasta shells (or blocks).” Make 4 equal groups and distribute objects into each until you have 20 total. Then emphasize: “We made 4 groups and ended up with 5 in each – that’s because 4 × 5 = 20, so 20 ÷ 4 = 5.” Visual demonstrations like this connect the dots between the two operations. (In fact, teachers often use array drawings or grouping diagrams in class for this very reason – it strengthens the multiplication-division connection by showing the same scenario in two ways.)
- Leverage fact families: As mentioned, fact families are a great way to highlight the connections. Pick a set of three numbers (like 6, 7, and 42) and have your child list out all the multiplication and division sentences involving them. Once they see, for instance, that 6 × 7 = 42, 7 × 6 = 42, 42 ÷ 6 = 7, and 42 ÷ 7 = 6, emphasize how knowing one fact unlocks the others. You can even make a game of it: give your child two of the numbers and ask them to figure out the third number that completes the family.
- Play multiplication-division games: Turn practice into play. For example, write some division problems on index cards and a matching set of multiplication problems on other cards (e.g., one card says “15 ÷ 3” and another says “3 × 5”). Lay them out and play a memory matching game where they have to find the pairs. Or simply quiz each other: you ask a division fact and they respond with the associated multiplication (or vice versa). Apps and games that emphasize fact families can be useful here too. (Monster Math, for instance, uses strategy-based practice to reinforce these connections, turning learning into a fun adventure.)
- Keep it light and encouraging: When your child uses the strategy successfully, celebrate it. If they get stuck on a division fact, gently remind them, “Try thinking of a multiplication that might help.” Over time, with positive reinforcement, they’ll gain confidence and see division not as a scary new challenge, but as a familiar friend in disguise.
Learn more about math strategies in these two guides - one for addition and subtraction and another for Multiplication and division.
Frequently Asked Questions (FAQs)
Q: Should my child memorize the division table, or just use the “think multiplication” strategy?
A: Think multiplication is a bridge to understanding and quick recall. By practicing the strategy, many division facts will become memorized implicitly over time. The goal is for your child to instantly recognize that, say, “8 × 4 = 32,” and therefore know “32 ÷ 4 = 8” just as quickly. Pure memorization without understanding can work for some kids, but research indicates it’s less effective for most. By focusing on multiplication connections, you ensure they grasp the “why” behind the facts. In short: use the strategy as a stepping stone – with enough practice, the knowledge will stick, and they’ll essentially have their “division tables” memorized anyway, with a deeper understanding to boot.
Q: At what age or grade should a child start using the think multiplication strategy?
A: Typically, children start learning basic multiplication in 2nd or 3rd grade, and basic division soon after (as part of the same fact families). As soon as your child knows some simple multiplication facts, you can introduce the idea that division is the reverse of multiplication. Even a second grader who knows that 2 × 5 = 10 can apply that to solve 10 ÷ 5. In fact, teaching the connection early on can prevent the two operations from feeling separate later. By 3rd grade, when division facts become a focus, students who’ve been thinking this way are at a huge advantage.
Q: What if my child struggles with multiplication facts? Will this strategy still work?
A: It’s important that your child has a handle on at least some multiplication facts first – the strategy builds on that knowledge. If they are still in the process of learning multiplication, continue working on those fundamentals (using fun strategies, not just rote drilling). You can still introduce “think multiplication” gradually: for example, if they know their 2s and 5s, start with division problems that involve those (like 10 ÷ 2, 10 ÷ 5, 20 ÷ 5, etc.). Success with easier facts will reinforce the strategy. As their multiplication fluency grows, the strategy will only become more powerful. It might also be a sign to use more engaging methods for multiplication – songs, games, or apps – so that the prerequisite facts stick better. Remember, multiplication and division fluency develop hand-in-hand, each reinforcing the other.
Q: Is “think multiplication” just a trick, or is it an officially recommended strategy?
A: It’s absolutely a research-backed strategy. Math education experts (and many school curriculums) explicitly recommend leveraging the inverse relationship between multiplication and division to help children learn their division facts. Far from a “trick” that bypasses understanding, it actually builds understanding by highlighting how the operations are connected. You can confidently use this approach knowing it’s aligned with modern teaching practices and supported by studies.
References
- Burnett, J. (n.d.). Developing the Essential Strategies for Computation. ORIGO Education. (Professional learning document by math educator James Burnett. Explains that because multiplication and division are inverse operations with an equal-parts total structure, “using multiplication is the most effective thinking strategy for helping students learn the basic division facts.”)
- LeFevre, J. & Morris, J. (1999). More on the relation between division and multiplication in simple arithmetic: evidence for mediation of division solutions via multiplication.Memory & Cognition, 27(5), 803–812. (A psychology study demonstrating that adults often solve division by referencing multiplication. Participants in the study would “recast” division problems like 56 ÷ 8 into the multiplication 8 × 7 = 56, supporting the idea that division facts are frequently retrieved through multiplication knowledge.)
- Szkudlarek, E., Zhang, H., DeWind, N. K., & Brannon, E. M. (2022). Young Children Intuitively Divide Before They Recognize the Division Symbol.Frontiers in Human Neuroscience, 16:752190. (Research finding that children ages 6–9 could perform approximate division tasks even before formal instruction. Notably, some kids who didn’t yet recognize the ÷ symbol could still intuitively solve fair-sharing problems, indicating that an intuitive sense of division precedes formal learning.)


Comments
Your comment has been submitted successfully!