Concrete - Representational - Abstract (CRA) Ladder for Dyscalculia: Step-by-Step Guide

TL;DR

If you're a parent in the US with an elementary school child struggling with math, or a teacher in a neurodiverse classroom, you know how challenging it can be to find effective ways to support learning. Dyscalculia, a specific learning disability affecting number sense and math skills, impacts about 3-7% of students. It can make everyday math tasks feel overwhelming.

However, there's hope in evidence-based strategies like the Concrete-Representational-Abstract (CRA) method. This approach, often called the CRA ladder, helps build a strong foundation by starting with tangible experiences and gradually moving to abstract concepts.

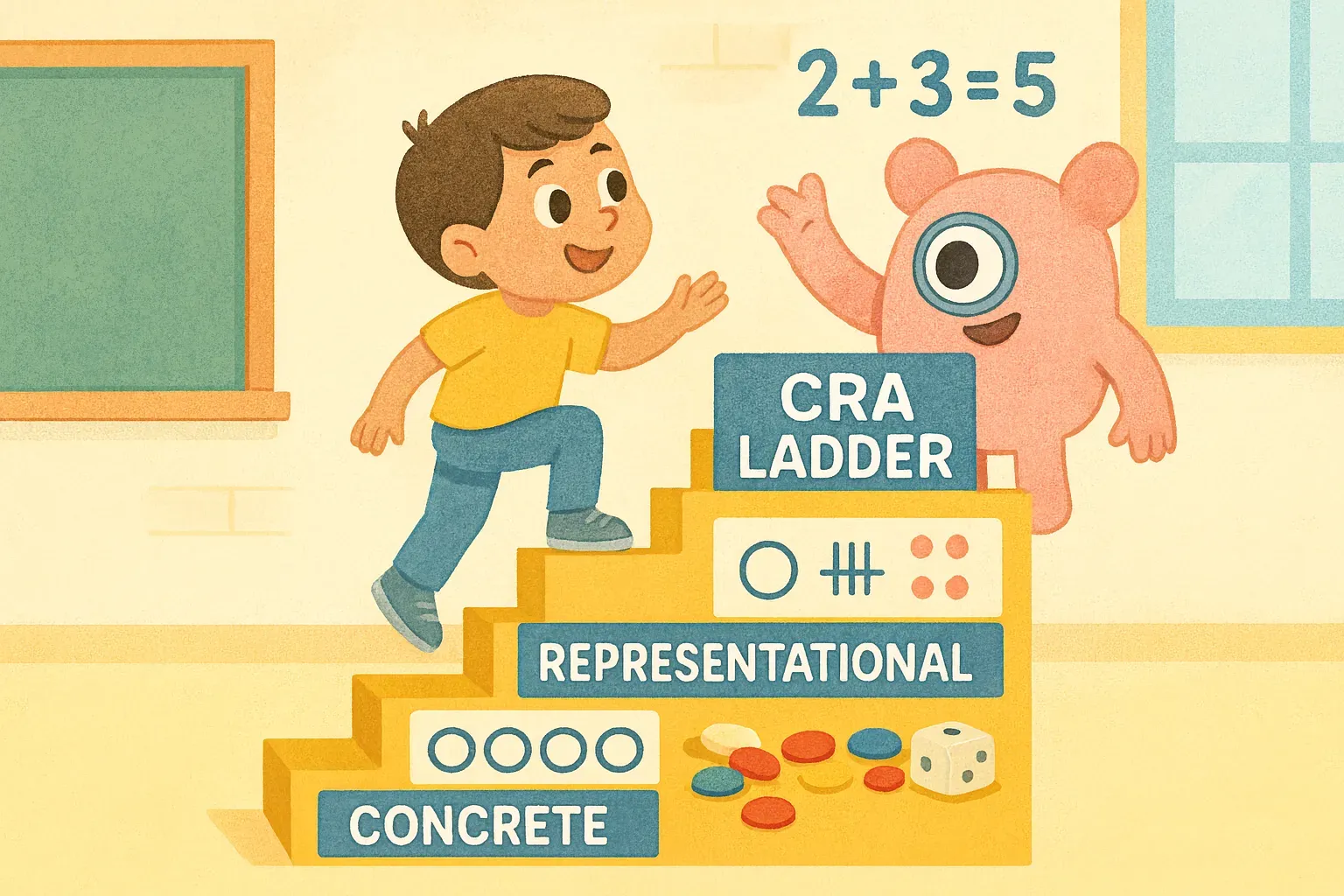
In this guide, we'll explore what CRA is, why it may help children with dyscalculia, and provide a step-by-step implementation plan - along with specific tips for kids with dyscalculia. Everything here is supported by peer-reviewed research on CRA and multisensory strategies, ensuring you have reliable information. We'll also touch on how this fits into broader math education for neurodiverse kids. 

For more on identifying challenges, check out our post on signs your child may have dyscalculia and how to help.

Understanding Dyscalculia in Elementary School

Dyscalculia is a developmental learning disability that affects a child's ability to understand numbers and perform math calculations. According to research on students with mathematics learning disabilities, it often manifests as difficulties in distinguishing shapes, understanding measurements, or solving word problems. In elementary school, this might look like trouble with counting, basic addition/subtraction, or grasping concepts like place value.

For parents, it's important to recognize that dyscalculia isn't about laziness - it's a neurological difference. Teachers in inclusive classrooms see this in neurodiverse students, where traditional rote learning falls short. Evidence from studies on CRA in inclusion classes shows that tailored approaches can lead to better retention of math knowledge, even in complex topics like algebra basics.

What Is the Concrete-Representational-Abstract (CRA) Method?

The CRA method is a structured teaching sequence that builds math skills through three progressive stages: concrete, representational, and abstract. Rooted in cognitive development theories, it aligns with how children naturally learn by moving from physical experiences to symbolic thinking. As explained in guidance on CRA instructional sequences, this approach enhances performance by connecting concepts across levels.

Why does this matter for dyscalculia? Multisensory strategies within CRA engage multiple senses, helping children with procedural learning deficits build stronger neural pathways for math.

Why CRA Works for Children with Dyscalculia: Evidence from Research

Research indicates that CRA can be effective for students with learning disabilities, including those with dyscalculia. For instance, a study on teaching perimeter using CRA found significant improvements in performance among students with mathematics learning disabilities, with skills retained weeks later. Participants showed moderate effect sizes, suggesting the method helps reduce error patterns and build conceptual understanding.

Another comparative study on CRA for pupils with dyscalculia demonstrated that both CRA and explicit instruction led to higher post-test scores, with no gender differences, highlighting its broad applicability.

In inclusive settings, CRA in Algebra I classes improved knowledge retention, though student perceptions varied - some found it confusing at first, underscoring the need for patient implementation. For neurodiverse classrooms, this means CRA can bridge gaps without stigmatizing students. Even though this study was for middle school kids, the pedagogical concept generalizes to elementary kids as well. 

Pairing CRA with tactile math activities or games can further enhance engagement.

Step-by-Step Guide to Implementing the CRA Ladder

Let's break down how to use CRA at home or in the classroom. Focus on elementary topics like addition, subtraction, or fractions. Always start slow, ensure mastery (80%+ accuracy) before advancing, and use positive reinforcement.

Step 1: The Concrete Stage (Hands-On Learning)

In this "doing" phase, use physical objects to represent math problems. Research on CRA sequences emphasizes manipulatives like blocks or chips to model concepts.

Example for Addition (2 + 3 = 5):

• Gather materials: Use counters, blocks, or even household items like buttons.
• Model: Show two buttons, add three more, count together.
• Practice: Have your child manipulate the objects and verbalize ("I have two, plus three makes five").
• Tip: For dyscalculia, this stage reduces abstract overload, as multisensory research shows tactile input aids memory.

Duration: Several sessions until mastery.

Step 2: The Representational Stage (Visual Drawings)

Transition to drawings or pictures. Studies on CRA for basic operations note this stage helps generalize skills.

Example for Subtraction (5 - 2 = 3):

• Materials: Paper, crayons.
• Model: Draw five circles, cross out two, count remaining.
• Practice: Child draws and explains.
• Tip: Link back to concrete— "Remember how we used blocks? Now we're drawing them."

This stage builds visualization, crucial for dyscalculia, per perimeter studies.

Step 3: The Abstract Stage (Symbols and Equations)

Move to numbers and symbols. Inclusion class research shows this leads to retention.

Example for Place Value (342):

• Model: Write 300 + 40 + 2 = 342.
• Practice: Solve equations without visuals.
• Tip: Revisit earlier stages if stuck.

Integrating Stages: Full Ladder Example for Fractions

For halves (1/2):

• Concrete: Split a candy bar.
• Representational: Draw a divided rectangle.
• Abstract: Write 1 ÷ 2 = 0.5.

Fraction research within CRA supports this for struggling learners.

Tips specific to Dyscalculia

1. Start small: Choose one concept per week. Use apps like Monster Math for reinforcement - see our guide on building number sense. Monitor with simple tests, celebrate progress. In classrooms, group activities foster inclusion.
2. Especially for dyscalculic kids - it would help to stay in the concrete and representational stages longer - so they build a much stronger foundation before moving to the abstract stage that they can find difficult.
   
   Potential challenges: Some kids may resist manipulatives, but perception studies suggest explaining benefits helps.
3. Use large, high-contrast manipulatives, reduce visual cluter when kids are in the concrete phase. 
4. Instead of seeing these stages as "sequential" - and moving from concrete to representational to abstract - keep the concrete and representational materials always ready even as the child is in abstract stage. Having all the modes together can help kids with dyscalculia significantly by creating multiple access points. 
   
   For example while doing word problems, help them visualize the word problems to picture scenarios; or even use physical manipulatives to represent the word problem first before attempting to get the answer. 
5. Normalize usage of manipulatives and integrate joyful elements like modified games. This can help reduce math anxiety which could lead to avoidance.